Question
This is a most asked interview question in Microsoft :). Rotate an NxN array 90* clock-wise. Give code for both using extra storage and not using it.
Answer
Using extra storage is easily predictable.
Consider a 3x3 array,
1 2 3 | 0 i
4 5 6 | 1
7 8 9 | 2
-------------
j –> 0 1 2
The rotated array will look like this:
i 0 | 7 4 1
1 | 8 5 2
2 | 9 6 3
----------------
j-> 2 1 0
You can see how the j is inverted to get the 90* rotation.
Usually, if you put a iteration like this,
for(i=0;i<N;i++) {for(j=0; j<N; j++){// A[i][j]}
}
You get rows traversed from top –> bottom. The movement is left->right.
In our rotation case, we have to come from bottom –> top. The movement is still left->right.
But to do the above kind of movement we need extra array of equal size.
Code
In our rotation case, we have to come from bottom –> top. The movement is still left->right.
But to do the above kind of movement we need extra array of equal size.
Code
int** rotate(int** arr, int N)
{int** b = (int**)calloc(N, sizeof(int));
for(int i=0; i< N; i++)
b[i] = (int*) calloc(N, sizeof(int));
for(int i=N-1; i>=0; i--)
{for(int j=0; j < N; j++)
{b[j][(N-1)-i] = arr[i][j];
}
}
return b;}
void printArray(int** arr, int N)
{for(int i=0;i<N;i++) {
for(int j=0;j<N;j++)
std::cout<<arr[i][j]<<" ";std::cout<<std::endl;
}
}
void main(){int N=4;int** rot90;int c=1;int **A = (int**)calloc(N, sizeof(int*));
for(int i=0; i<N; i++) {
A[i] = (int*) calloc(N, sizeof(int));
for(int j=0; j<N; j++) {
A[i][j] = c++;
}
}
printArray(A, N);
rot90 = rotate(A, N);
printArray(rot90, N);
}
Important points:
- In above code, b[j][(N-1)-i] is required to copy top->bottom into b[] from bottom->top of arr[]
- (N-1)-i is required to convert the coordinate which moving from bottom to top, to move top to bottom.
- j loop is the main loop which performs the rotation
- the above code cannot be reused for in-place since it replaces the contents of the array
If we want to do without space, there is one more tricky and tough to guess approach.
The below diagram is for a 4x4 matrix on how to swap array contents in-place to achieve a 90* rotation.
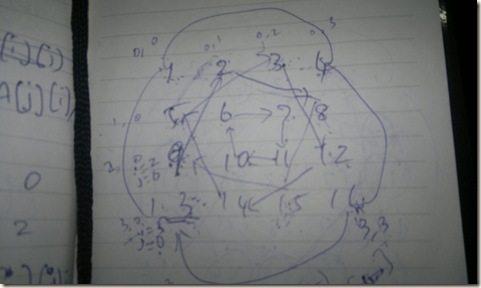
We first do a outer shell swap and then move to the inner circle. Thinking this logic is simple, but putting it in code is not so simple for a dummy.. :)
If you do this in code as well, you might get more tougher questions :D
void printArray(int** arr, int N)
{for(int i=0;i<N;i++) {
for(int j=0;j<N;j++)
std::cout<<arr[i][j]<<" ";std::cout<<std::endl;
}
}
void rotate_inplace(int**& arr, int N)
{//find the number of circles or shells in our matrix// in a 5x5 matrix, the total circle is 2// in 3x3 matrix, the total circle is 1for(int shell=0; shell < N/2; shell++)
{//for each shell, perform 4-way swapint i=N-1-shell; // for 4x4, 3
int j=shell; // initial 0
for(int k=j; k<i; k++)
{int movement = k-j; // initial, 0, movement in a shell
int top = arr[j][k]; // left most corner node
// top <- rotation start nodearr[j][k] = arr[i-movement][j];
// rotation start node <- right most corner nodearr[i-movement][j] = arr[i][i-movement];
// right most corner node <- top right cornerarr[i][i-movement] = arr[k][i];
// top right corner <- toparr[k][i]=top;
}
}
}
void main(){int N=4;int** rot90;int c=1;int **A = (int**)calloc(N, sizeof(int*));
for(int i=0; i<N; i++) {
A[i] = (int*) calloc(N, sizeof(int));
for(int j=0; j<N; j++) {
A[i][j] = c++;
}
}
printArray(A, N);
rot90 = rotate(A, N);
printArray(rot90, N);
rotate_inplace(A, N);
printArray(A, N);
}
- We cover a full shell in each iteration. Total shells in a NxN matrix is always N/2
- At each shell we get the min and max size of the shell. i holds the max size, j holds the min size
- k is the iterator which iterates from shell min size to max size. So, for a 4x4, the outer shell will have min size 0, max size as 3. k will run from 0 to 3
- min size and max size also set the corners of the square shell. You think that, the square starts at min size coordinate and ends at max size coordinate.
- As the k loop continues,
- the top holds the top line of of the square shell always (based on k value)
- arr[i-movement][j] takes the left side line of the square ( based on movement)
- arr[i][i-movement] takes the bottom line of the square(based on movement)
- arr[k][i] takes the right line of the square (based on k value)
- Pictorially, there are 4 points in a square in a 4x4 matrix and all if connected forms another square.
- movement size will get reduced in inner shells.
- The loop exit condition is very important. As we know that the matrix is 4x4, we know that it has total 2 shells. So, we can stop after processing 2 shells.
Without space(easier way)
EDIT: Just change rows to columns, columns to rows by just swapping. After your swapping is done, you will get an array in which all rows has became columns and all columns would be rows. In this array, swap column-wise first and last. and continue until you reach the middle. You get 90* rotated array as final output. But performance is little bit more with same amount of swaps.
No comments:
Post a Comment