Binary manipulation

The basic computer course starts with 0 and 1 which is the only understood words by any digital machine. These 0 and 1 are nothing but a square wave created for a digital signal. Very clear and crisp, beep high, beep low CRO sound is what a computer is. But no one understands the math behind this.

"There are 10 kinds of people in the world,
those who understand binary numbers, and those who don't.”

Credits & Reference

http://www-graphics.stanford.edu/~seander/bithacks.html

History

  The basic granularities in a computer is bit which is 0 and 1. Then you have a byte which is 8-bit size. This goes on in multiples of 1024 until petabyte. There are different names used to represent the size used as move forward with 32-bit and 64-bit processing machines. Remember we started with 4-bit machine used in calculators (Intel 4004), then came a 8-bit processor family (Intel 8080), 16-bit processors (Intel 8086), 24-bit processors (IBM PC/AT), 32-bit processors (now called i386,i486, Intel 80386) and finally 64-bit processors (AMD Athlon).

  Since such multiple architectures came into picture, the sizes are represented as WORD, DWORD, QWORD. Usually, WORD is 16-bits, DWORD is 32-bit and QWORD is 64-bit. But for backward compatibility and system architecture limitations this size varies.

Math behind binary

   Binary is considered as a base 2 number system. Our decimal system is a base 10 number system. Representations of number systems is explained in detail in number theory subject of mathematics.

Read here: http://www.mathsisfun.com/binary-number-system.html

Similar to a decimal system where we have floating point, we can represent binary as well in a floating format.

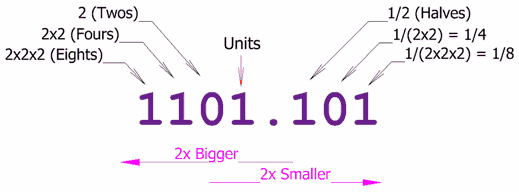
Note that, at the left multiplication of 2 happens and after the decimal point to the right division of 2 happens.

Now, some ground basics. Any decimal system as i said will have the same following properties.

• The number of symbols in the system is called the ‘base’
• All the number systems has some ‘precision’ associated with it
• There are negative and positive numbers in it
• If it is a number system with a base, it can be represented using logarithms

The logarithm (or log) of a number to a given base is the power to which the base must be raised in order to produce that number.^[1]

Logarithms are generally used to reduce multiplications and divisions recorded in olden days. They are still used to represent large numbers. :)

In computers, mostly large binary numbers are represented as, log₂n which is 2ⁿ. When it comes to binary, logical operations are also possible on them. Some of the logical operations are like AND, OR, NOT, XOR.

What all can be done by bit manipulations ?

   There are many operations present in computers which can do bit manipulations do take care of multiplications and divisions. The most common bit manipulations easily done are:

• Left shift by 1 = divide by 2 (decrease the number of bits by 1)
• Right shift by 1 = multiple by 2 (increase the number of bits by 1)
• AND/OR is used for masking and extracting a single bit (used for reading/writing flag registers)
• NOT is used for toggling bits (mostly used to set a flag true or false)
• XOR can be used for swapping and comparisons (for testing difference between two numbers fast)

Important interview questions

• Counting bit set in a integer
• Compute the parity bit for an integer (to detect errors in transmission http://en.wikipedia.org/wiki/Parity_bit). Very important question in a networking related field
• Swapping values with subtraction and addition (one of my favourite question asked by one of friend :) )
• Swapping values using XOR
• Reverse the bits in a value
• Compute the modulo division without division operator (asked in cryptography field)
• Find the log base 2 of an integer without any extra libraries
• Count the number of trailing zeros in a integer
• Test for null byte in a byte stream in a faster way
• Number of possible permutation for a binary number to be represented with swapping 1’s. For example, if N is 3 and the bit pattern is 00010011, the next patterns would be 00010101, 00010110, 00011001,00011010, 00011100, 00100011, and so forth.

Study about all the above methods in this link: http://www-graphics.stanford.edu/~seander/bithacks.html