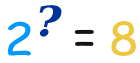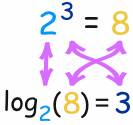“Beauty of quick sort is, its so quick!!.. unlike other sorting algorithms based on divide and conquer, where divide, conquer, combine all are independent steps. In quick sort, divide and combine are done in one-shot. i.e, just divide actually sorts the whole array!!”
See Also
http://analgorithmaday.blogspot.com/2011/02/partitioning-algorithmin-place.html
Introduction
Quick sort is the mostly discussed and used algorithm in any code that you have written. That’s why its the simplest interview question to be asked!! :). If even this cannot be answered, then you will be thrown out. The first important step is partitioning. Please study the above link fully!!
Multiple partitioning is what quick sort does. But while doing multiple partitioning, it reduces the input set given for partitioning. So, partially sorted array at both the side of a partition, again gets partitioned further.
Concept
The important concept to be understood in a quick sort is that, we take each and every element in the array as pivot to get the final sorted array. It’s not possible to take one element as pivot and sort the whole array!!.. As a dummy, i too thought like that, but its not the case.
Take for example,
13 4 5 6 11 10 2
Partition=1: pivot=2,
13 4 5 6 11 10 (2)
Partition=2: pivot = 10
4 5 6 (10) 11 13
Partition=3: left, pivot=6, right pivot = 13
4 5 (6) 11 (13)
Partition=4: left pivot=5, right pivot=11
4 (5) (11)
Ignore the pivots in each partitions.. to decide the next pivot. This is also the main concept of quick sort!!
The tree representation,
13 4 5 6 11 10 (2)
/ \
4 5 ( 6) (10) 11 (13)
……….. Check some reference books to get a perfect quick sort tree..!! :)
So, final sorted list is, 2 4 5 6 10 11 13.
But note that, we don’t partition single element arrays.. :) That is base condition for quick sort. And also you could see that, the pivot rearranges the array, so if you consider a tree, it will be like, go from top to bottom to partition, to get all sorted, go from bottom to top!!..But pivots should occur in order, they are in the initial tree shown above!! But note that, all elements become a pivot!!
Code
void swap(int& a, int& b)
{ register int tmp;
tmp = a;
a=b;
b=tmp;
}
int partition(int* arr, int start, int end)
{ /*
1. decide a pivot element, let it be arr[end]
2. categorize arr the remainting start -> end-1
3. consider 2 indeces = i,j: initially i=start-1, j=start
4. make sure that i+1 to j-1 always contains element > pivot
5. the above means, i marks end of smaller elements array
6. j marks the end of larger elements array
*/
/*
Example:
start=0 end=12
i=-1 j=0
3 6 2 1 9 4 12 19 13 10 8 5 11
After you do this partition,
start i j end
3 6 2 1 9 4 10 8 5 [11] 12 19 13
The important point here is, after 4, we see 8 which is < 11.
So, it needs to be inserted.
Because of the above point we need 2 indeces.
*/
int i,j, pivot;
pivot = arr[end];
i=start-1;
for(j=start; j<=end-1; j++)
{ if(arr[j] <= pivot) { i=i+1;
swap(arr[i], arr[j]);
}
}
swap(arr[i+1], arr[end]);
return i+1;
}
void quick_sort(int* arr, int start, int end)
{ if(start < end) { int mid = partition(arr, start, end);
quick_sort(arr, start, mid-1);
quick_sort(arr, mid+1, end);
}
}
void main()
{ int A[]={3, 6, 2, 1, 9, 4, 12, 19, 13, 10, 8, 5, 11}; int B[]={6,10,2};
//sorting 3 elements
quick_sort(B, 0, 2);
//sorting more elements
quick_sort(A, 0, 12);
}
Important notes
- quick sort has the perfect predictable average case of theta(n log n).
- quick sort also has Theta(n2) worst case. Merge or heap sort is the best algorithm since even worst case is O(n log n). But, merge or heap sort has space complexity, bad average case and large constant time!!
- quick sort performs in its worst case when the array is sorted!! its because, all the splits will be bad!!.. always you will have the pivot at the end!!..
- If the pivot is at the end, even after the split, its a bad split!!.. good split means, you get the pivot at the middle after a partition
- To do quick sort in descending order, just change the <= to >= in partition code!!
