Selection sort & Bubble sort

“Selection sort would have invented when a beautiful mermaid sat and sorted different sized pebbles by pure selection. Compare the full pebble collection and pick the smallest out first.. continue until you get different sized pebbles arranged”

Metaphor

   This is the simplest algorithm and also very important algorithm which has different use cases. Metaphor is the same as the quote. Even your grandma would do this sort in daily life, removing stones out of a rice crunch, organizing smaller to bigger bottles in the kitchen, arranging smaller books to the bigger books purely based on selection. Our mind by default uses selection sort to do day-to-day sorts.

Concept

Wikipedia explains this concept very clearly with the below image,

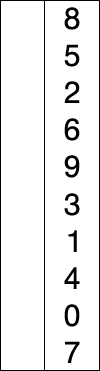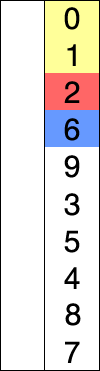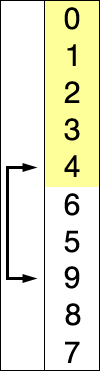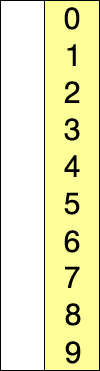
There is a monkey sort everyone learns named Bubble sort, which compares each number with each other and swaps. Selection sort swaps only after finding the minimum index in the list under study.

Bubble sort is heavily discouraged by everyone. Even interviewers don’t ask questions related to it since even college pass-out treats this as an personal insult.  

Code

   1:  void bubble_sort(int* arr, int size)

   2:  {

   3:      int temp;

   4:      for(int i=0;i<size;i++)

   5:      {

   6:          for(int j=0; j<size;j++)

   7:          {

   8:              if(arr[i] < arr[j])

   9:              {

  10:                  temp = arr[i];

  11:                  arr[i] = arr[j];

  12:                  arr[j] = temp;

  13:              }

  14:          }

  15:      }

  16:  }

  17:  void main()

  18:  {

  19:      int A[]={3,41,52,26,38,57,9,49};

  20:      bubble_sort(A,8);

  21:  }

In the above bubble sort, note the amount of swap done and the total count of operations which is O(n²) which is why people avoid this algorithm altogether. Important notes for even writing this code, I am such a dummy you know

Note:

1. swap never follow any order and swap operates only on indexes. So, You can store arr[i] or arr[j] either of them in temp. i.e, if a[4]=32, a[2] =24 needs to be swapped, don’t confuse with value, see the index 4->2, 2->4 is what happens whatever value they hold the condition safe guards it. Since, a[4] > a[2], the swap won’t happen and only when a[2] < a[4] becomes true, swap happens. So just converting the lesser symbol to greater symbol makes it sort in decreasing order. Note that most of the sorting algorithms have this property.

2. Why swap is so complex? try removing the condition which safeguards swap and check what happens. It gives you something like a dice thrown upon the array. But its not random. Believe me!! It rotates the array by 2 (since its 8*8 rotations along each index) . This will become an interview question . We will discuss this rotations inside an array in far future.

   1:   

   2:  void selection_sort(int *arr, int size)

   3:  {

   4:      int imin = 0;

   5:      int temp;

   6:      for(int i=0; i<size;i++)

   7:      {

   8:          imin = i;

   9:          for(int j=i+1;j<size;j++)

  10:          {

  11:              if(arr[j] < arr[imin])

  12:              {

  13:                  imin = j;

  14:              }

  15:          }

  16:          //swap

  17:          temp = arr[i];

  18:          arr[i] = arr[imin];

  19:          arr[imin] = temp;

  20:      }

  21:  }

  22:   

  23:  void main()

  24:  {

  25:      int A[]={3,41,52,26,38,57,9,49};

  26:      selection_sort(A, 8);

  27:  }

Problems in a selection sort, swap is orderless. So, don’t care. Store only the index where minimum is found and assume ‘i’ as the minimum index at each loop. You need values only for the swap. Even that can be simplified, if there is a routine for swap which takes index.

Important points

• Selection sort has use cases when u just need the minimum values first. There is a data structure called Min Heap which returns minimum value from a heap always. Such data structures operate based on selection sort.
• Selection sort has same complexity equal to bubble sort O(n²). But performs better than bubble sort. But usually all quadratic time algorithms are avoided in real time and large scale projects.
• Read again and review insertion, if you had forgotten by now (i did)http://analgorithmaday.blogspot.com/2010/12/insertion-sort.html 
• In Insertion sort, we select a number in an unsorted list and scan the already sorted list. So, it is faster than Selection sort. But still its O(n²). Speed comes with the difference in the constants that gets hidden with the above notation.