The mathematics behind a binary tree

“We have not seen the true mathematics behind a tree in brief. We shared a video about tree studies and directly dived into Heap (which is also known as binary heaps)”

Metaphor

  As I forgot about the whole tree concept after finishing full heap section and n/2 formulas, I wanted learn the real math that governs atleast the binary trees. What is that log n? What is that 2ⁿ? How it is calculated?

  Unlike the real tree, there are numerous kinds of trees in computers. The most usable tree is a binary tree because it has properties which are easy to process in unit time under the same computer base “2”.

  Why binary tree is called binary? Because it also operates on base “2” similar to a binary system.

It would be like a Nuclear reaction in which One big uranium atom splits into two, then these two split into 4, and then 8..

Concept

   On every growth from root, you get powered increase to 2.

                   1               ------------> 2⁰

             2            3       ------------> 2¹

          4    5       6   7    ------------> 2²

This means at each level, you get 2^level nodes. Then what would be the total number of nodes,

2⁰ +2¹ + 2² + 2³ +….+ 2^h = 2^h+1 – 1

where, h is the height of the tree. But its funny!! how this formula came at first account!!

If you note at each level we get 2’s increased in the multiplication, 2, 2*2, 2*2*2.. etc.. The important thing is, 2*2*2 has 2*2 and 2 as well!!..Which means 2^h+1 covers all the multiplications. But what is –1? The whole binary tree has 2 nodes always after the root node!!.. only the root node is odd numbers (only 1 element). With the above calculation, we consider root also as “2”.

That’s why, 2^h+1-1 gives the exact count of nodes. So from all this, we know that, at any level, we have 2^h nodes.

Which means, at leaf, we also have 2^h nodes. What is log n then? if 2^h nodes are there, how to represent it in logarithms?

  log n = 2^h

where, n is the number of nodes.  Its like how many 2’s are there for each h to form n. Mostly we subtract 1 from it, as root might also be taken as two at the end.

Important observations here:

• The leaf covers half of the tree.. as you can 2³ gives 8 nodes which is almost equal to the top half 7. That’s why in heap building, we consider leaf start at n/2 + 1. This 1 is to cross the root.
• Root is the only odd count in the whole tree.
• The most common types of trees like full, perfect, complete, balanced

More information

full binary tree – all nodes, even the root should have two nodes. It looks like a dancing tree, LEFT tree can be bigger than the RIGHT tree.

perfect binary tree – it’s a full binary tree, but must be a perfect christmas tree. No left or right tree growth. This is the strictest tree!!

complete binary tree – other than leaf level, all levels should be filled with nodes.

The complete binary tree is the most confusing and mostly used one!!

The above is the complete binary tree. At leaf level, you don’t have one node. But its still ok for it.. This is what used for binary heap!!. Binary heaps, heap algorithms all constructs a complete binary tree on the array!!

Another important concept in a tree is, NULL links!!!

NULL links are so important that in future we use that to convert a tree to linked list and explain a concept called threaded tree!!.

What is a null link?

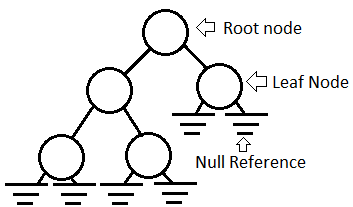
Similar to a circuit ground, NULL links are important and usually not denoted one in a tree!!..

Some important properties of complete binary tree:

The number of NULL links in a Complete Binary Tree of n-node is (n+1).

The number of leaf nodes in a Complete Binary Tree of n-node is UpperBound(n / 2).

For perfect and full, its very easy to find the above values since the leaf node set never go empty!! and the count of nodes at any level is always 2^h . NULL link count is different in full binary tree!!.. it will be 2*<number of leaf nodes>

Reference

http://en.wikipedia.org/wiki/Binary_tree