“I never understood concepts like permutation, combination which is quite confusing. But permutation is nothing but just a way to count all possibilities of a nested iteration!!”
Introduction
Just take, the following nested for loops
Simply we can tell directly the total iterations are m*n. But the traversal done by the loop with an array will be like..
REPEAT –> read the row –> read from left to right –> move to next row –> UNTIL i*j == m*n
These are the various values comes out considering m=3, n=3,
{0,0}, {0,1}, {0,2}
{1,0}, {1,1}, {1,2}
{2,0}, {2,1}, {2,2}
Keeping i, we iterate with changing symbols in j.. Doesn’t it look like Cartesian Product with a Condition?
This kind of rearrangement of numbers are necessary to traverse the array. Similarly you need rearrangement of numbers in various applications!!..
For example, say, you need to find all possible rearrangements of a shuffled 56 deck card.. There are numerous ways if you need to find the rearrangements of all the 56 cards(56!).. But if you want to know rearrangements possible when the cards are distributed within 14 people..
You just need to count 14 possible rearrangements out of 56 cards to calculate. This is where you need permutation..
To understand permutation well, you need to understand set theory!! Especially Cartesian Product!.. Learn about set theory first: http://analgorithmaday.blogspot.com/2011/05/set-theorya-dummies-guide.html
Concept
Every multiplication can be represented with a set of additions. When you add a number that much times, you get the multiplied value. Similarly, if you have a set of 3 numbers.. how would need to find the number of ways it can be rearranged?
Strings
If you take Cartesian product of same set k times with each set having some n symbols in it, you get strings. S^k sets with each having n items.
i.e, If the set is S, S x S x S is a 3-set product. If you have only 2 elements in it, then total you get 2^3 distinct elements as a result of this product. This count of distinct elements can be got from n^k equation. Example, Take a binary string of length 3. You have max 2 symbols possible in a binary. Total possible sets are,
000,001,010,011,100,101,110,111
Which is 2^3.
Permutation
Permuting means, simply re-arranging without missing any symbols!!.. if you want the number of rearrangements what would you do ? That’s where permutation comes into picture.
For example, saw you have a set {a,b,c}. The total number of ways, you can order this variables are,
abc, acb, bca, bac, cab,cba
Total 6 ways, the above 3 char array can be permuted. This gives as a pattern, the first element is chosen n ways, the next ignoring the first element chosen in n-1 ways, the next in n-2 ways. This means, you get n(n-1)(n-2) which is nothing but n!
If in the same above array, you just need to know the permutation of only k-elements instead of all n elements. (n is the total elements in the array). ex: this is similar to finding the 14 cards possible rearrangements in 56 card deck..
then, the total ways are,
ab, ac, bc, ba, ca, cb
Again the same, 6 ways. But now, n, n-1, n-2 and upto n-k+1 is what required. So, The formula becomes like below,
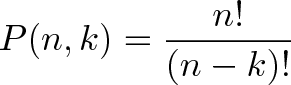
Combination
We already saw about Strings which we get by Cartesian product of the same set and get the unique items out of the set with each symbol in an order.
Combination has the same property of getting unique items with each item at one place but ignores the order of items requirement. It considers symbols in both the set and takes out in-order uniquely!!.. i.e, You should remove transitive, symmetric symbols in a combination!!
Ex: Permutation for 2 element in a 4 element set, {a,b,c,d}
ab,ac,ad,ba,bc,bd, ca,cb,cd,da,db,dc
Total 12 sets are possible since we need to consider every re-arrangement in any order.
Combination for 2 element in a 4 element set, {a,b,c,d}
ab, ac, ad, bc,bd, cd
There are only 6 sets!!.
Formula:
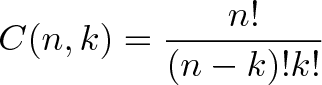
Examples
Some real world example!!
http://betterexplained.com/articles/easy-permutations-and-combinations/
You have 8 players.. and 3 different cups to be won. Gold, Silver, Bronze. You give each cup to only one of the players and the cups will be given in the order, Gold->Silver->Bronze.
Gold: When you need to give Gold, you have all 8 players competing for it. So, total 8 options possible.
Silver: When you need to give Silver, you have already given Gold, so only 7 options possible
Bronze: When you need to give Bronze, you have already given Silver, so only 6 options possible.
Total ways in which the 8 players can win will be 8! ways..
But, there are only 3 cups, so Total ways in which the top 3 cups can be won, if given one-by-one in order to the persons will be: 8 * 7 * 6.
This is where Permutation comes into Picture!
If the price money is same, i.e, a Stainless steel plate. You don’t need to care about the order in which the 3 cups are given. So, its 3 cups given to 8 players. But 3 cups re-arrangement don’t need to be taken into account as all are equal. So 3! ways of arranging the cups(6 ways) are useless when it comes to just picking some 3 out-of-8.
This is combination and you get only: 8*7 ways according to the formula.
No comments:
Post a Comment