Random number generation logic - Linear congruential generator

“Randomness is really important for probabilistic actions. Like card shuffling, coin tossing etc. How can we represent that in a machine? There are lot of random number generators available!!”

Introduction

  Random number generators have huge application space mainly in Cryptography. But we need this random number generators for the articles we will soon start studying about, HASH TABLES!! :) You need random unique keys for storing the values so that search is O(1) similar to an array.

  There are types of randomness however!! Pseudo Randomness & “True” Randomness!!.. All proven with heavy mathematical theorems. “True” Randomness is really important for security algorithms like RSA. But if the randomness fails and a pattern appears, you get to crack the security system as well!! :)

   Randomness is mystic and same as how our universe behaves :) So impossible to get true randomness without leaving it to run around the world.

  Watch this movie to understand how tough it is.. :) It’s about a Math scientist trying to find patterns and suicides with a head gun shot http://www.imdb.com/title/tt0138704/ (Psycho movie.. Beware)

  Ok, into the business. let’s get into some simple random generators!!

Concept

       LCG – Linear Congruential Generator is a method to generate pseudo random numbers until a particular range. After that range, the numbers would start repeating. This range value is also called as “seed”.

 

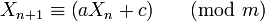
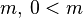— the "modulus"

— the "multiplier"

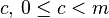— the "increment"

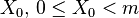— the "seed" or "start value"

Source: http://en.wikipedia.org/wiki/Linear_congruential_generator

The random value can go up to  MAX = “m”. single linear congruent equation usually repeats numbers. To avoid that, we have a multiplier “a”. We can either keep “c”, zero or non-zero.

If you have only “a”, then its called multiplicative congruential method.

Note that, the values of m, a, c decides the amount of randomness you get with this function. The values of these numbers are experimented and must have noted properties. :D

Refer the Wikipedia link for more details.

In C/C++, mostly we use time() function as the seed which gives us good precision. like below,

   srand(time(NULL));

After that, we set the modulus value “m”, by giving the rand a value,

   rand() % 500;

The above will generate a random number below 500 with X₀ = system time + the above suitable random multipliers. But you should note that, if you iterate 1000 times the above rand function, you will start getting the same numbers frequently.. we should get at least the first 500 times the different number!!.. But even that won’t happen :D

How this recursive function generated different numbers ?

The above plot will show you how the values get randomly distributed!!. Note that, this is happening just because m and a are prime..!!

Check more plots here: http://demonstrations.wolfram.com/LinearCongruentialGenerators/

Code

Try the below code:

void main()

{

    srand(time(NULL));

    for(int i=0;i<1000;i++)

        cout<<": "<<rand()%100<<endl;

}

I got the following last set of output with “8” straight-to-straight repeated. Just with a difference of some 2 extra iterations!!..

Output

: 8

: 18

: 37

: 8

: 33

: 14