Problem
This is project euler problem 14. Really interesting and mathematically challenging one.
The following iterative sequence is defined for the set of positive integers:
n 
n
Using the rule above and starting with 13, we generate the following sequence:
13
Source: Project Euler.
The below figure will explain the problem precisely.
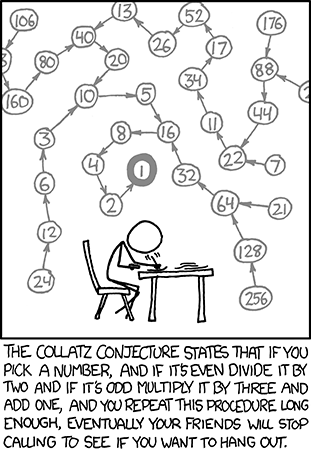
References
http://en.wikipedia.org/wiki/Collatz_conjecture
http://projecteuler.net/problem=14
Solution
I tried the tail recursive way first..!! But its too slow and it took hours to run.. In debug mode, stack is used even for tail recursion.. so, it went useless to do 1 million function calls every time. so, moved into a iterative way.
Just a brute force algorithm for 1 million values took around 10-15 minutes to run. But, the 1-minute rule given by project euler is not followed in this program.. :)
There are better ways to do.. But since there seems no valid applications for this series, am just leaving it here..
#include <iostream>
#include <cmath>
using namespace std;
int main(){ int gMax = 0; double gI = 0;for(double i=1; i<1000000; i++) {
double val = i; int count = 0; cout<<val<<" "; while(val != 1) {++count;
if (fmod(val, 2.0) == 0) {val = val/2;
}
else { // oddval = 3*val + 1;
}
}
count++;
if(count > gMax) {gI = i;
gMax = count;
}
cout<<endl;
}
return 0;}
- gMax is the maximum count of the numbers in the series
- gI is the number which yields this max count
2 comments:
//* Home Page: http://keith.pro/
//* Author: Keith Cancel
//* File Name: My_Version.cpp
//* Project: Collatz Conjecture in C++
//* Date: 12/8/2011
#include
using namespace std;
int main(){
//Starts on 2 and works its way up to 75 million.
//seems pretty quick took just a tadd over a minute to run 75 Million
//differnt starting numbers.
//keep track of how many loops
//Total loops at 75M is about 250 million shy of 13 billion loops.
unsigned long long count=0;
for(unsigned long i=2; i <= 75000000; i++){
int temp=i;
while(temp > 1){
//if odd multiple by 3 and add 1
//if even multiple by 2.
temp = (temp & 0x00000001) ? ((temp << 1)+temp+1) : (temp >> 1);
//Add one for every loop.
count++;
}
}
cout << "Total loops ran: " << count << endl;
}
Simpler way:-
#include
main()
{
int i,j,k=0;
printf("Enter a number ");
scanf("%d",&i);
k=i;
for(j=0;j<10;j++)
{
if(i%2==0)
{
k=i/2;
}
else
{
k=(3*i)+1;
}
printf("%d ->",i);
i=k;
}
}
Post a Comment