“During the periods of John Napier (http://en.wikipedia.org/wiki/John_Napier),
he was called a magician for inventing easier ways to multiply. But now, the
calculators and computers are the actual magicians for humans!!”
Introduction
As the above quote says, the history
behind logarithms is interesting and first we need to understand the problem
which made mathematicians to think about using shorter ways. Mathematicians are
seriously lazy people like us. :)
Napier had been working on his invention of
logarithms for twenty years before he published his results, and trigonometry
tables (sin, cos table) was the origin of his ideas at about 1594.He wanted to simplify
geometric progression by tabulating it and simplifying multiplications using
additions. With the additive property of powers as the concept behind his approach (2^1 * 2^2 = 2^3),
he started working out an approach to find a series for easy multiplication of
0.999. It was extended then to 10 in future.
10^1/2 = sqrt(10)
= 3.162277 which means log(3.162277) = ½. Similarly, We can continue for rational
powers easily, as 10^3/4 = 10^1/2*10^1/4 = sqrt(10) * sqrt(sqrt(10)) = sqrt(31.62277)
= 5.623413. which means log(5.623413) = ¾. I need to learn how sqrt values
moves decimal points. J But this
is how logs were calculated.
This means that recording powers of
a base present inside a huge number is what logarithms do.
More info
So simply,
logarithms is the record of power of a given value,
log 28
= 3 which means 2^3 = 8. Logarithmic tables recorded the powers of huge decimals with high precision and preparing such tables is tedious job!!
Below is the
logarithmic properties and b is the base.
- logb(xy) = logbx + logby.
- logb(x/y) = logbx - logby.
- logb(xn) = n logbx.
- logbx = logax / logab.
Example:
Log2 8
= log24 + log22
Log2 23
= 3*log22
Some diagrams from MathFun:
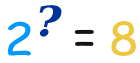
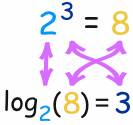
No comments:
Post a Comment