Tree insert & delete–Heap example!!

“As we move more and more, we see more and more of trees represented in arrays.. Wherever, double recursion is involved, you actually create a tree in an array. But double recursion just emulates array as a tree!!.. What about data structures that has tree kind of structure? Heap is one of this kind!”

See Also

http://analgorithmaday.blogspot.com/2011/01/tree-data-structureexplained.html

http://analgorithmaday.blogspot.com/2011/02/mathematics-behind-binary-tree.html

http://analgorithmaday.blogspot.com/2011/02/priority-queue-using-binary-heap.html

Introduction

   We recently studied about the maths behind binary trees specifically and different types of trees. But where would they really use all these trees? One use case is divide-conquer kind of problems where you deploy double recursion to create a tree on the stack. But we have not used tree as a data structure till now. Merge sort, Heap sort and whatever O(nlog n) sort that you can imagine just uses trees to divide and conquer. Then when we plainly represent and use trees: its plainly used on Priority Queues

   In Priority Queues, we studied lots of new ADTs and priority queue became nothing but a type of heap data structure. Even heap sort makes use of the heap’s properties and operations. So, its time to study heaps operations. Binary tree as such doesn’t need insertion, deletion plainly until there is a usable structure for it. So we wanted to take Heap as an example here,

• INSERT = add new element to the heap’s bottom
• DELETE = remove max element from the heap
• INCREASE_KEY = change the value to a higher value than existing
• DECREASE_KEY = change the value to lower value than existing

The above functions becomes readable in a tree’s construct only when it is linked with Heap.

Concept

      We studied max_heapify, heap_insert, increase_key already for heap sort as well as priority queue applications. Here, we gonna reuse the same concepts.

• Max heapify = bubble down, down heap is something which moves an element from top to bottom to satisfy max heap property. We move the element from top to bottom by comparing it with both LEFT and RIGHT
• heap_insert, increase key = bubble up, up heap is something in which we move an element from the bottom to top. We take the element from bottom to top by just comparing with the PARENT

If you note that, both the above routine inserts elements inside the heap and both perform almost equally (with some extra comparisons in max heapify). But both is used for different purposes sometimes.

Source: Wikipedia

Adding a new element to the heap

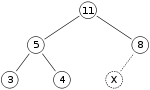
x=15 is the new element we need to insert

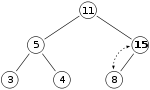
Compare with the parent and swap. Continue until the parent is lesser than the child.

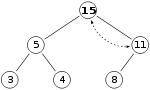
Finally, the root gets replaced with the new element added. This is up-bubbling which is carried out by out heap-insert procedure.

Deleting an element

This operation is similar to Heap-extract max routine we saw.

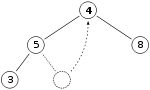
In the above diagram, we remove a max element say 15 from the heap. Since after we remove “15”, we assume the last element “4” as the root, since it would be somewhat least. So, we make “4”, the last node, as the heap’s root node

Now, it violates the heap property!!.. Do max-heapify to down-bubble the element.

Code

const int HEAP_SIZE=50;

#define PARENT(i)  (i-1)>>1

#define LEFT(x) 2*x+1 // since we start with index 0

#define RIGHT(x) 2*x+2

class MaxHeap

{

    int arr[HEAP_SIZE];

    int count;

public:

    MaxHeap() 

    {

        count=0;

    }

    bool insert(int element);

    bool remove(int& element);

    bool increase_element(int element, int idx);

    bool decrease_element(int element, int idx);

    bool change(int element, int idx);

};

bool MaxHeap::insert(int element)

{

    if(count > HEAP_SIZE)

        return false;

    int i = count;

    arr[i] = element;

    // the below loop never runs if the input

    // array is already in maxheap format!!

    while(i>0 && arr[PARENT(i)] < arr[i]) {

        int tmp=arr[PARENT(i)];

        arr[PARENT(i)] = arr[i];

        arr[i] = tmp;

        i = PARENT(i);

    }

    count++;

    return true;

}

bool MaxHeap::remove(int& element)

{

    if(count < 0)

        return false;

    element = arr[0];

    arr[0] = arr[count-1];

    arr[count-1] = INT_MIN;

    count = count - 1;

    max_heapify(arr, 0, count);

    return true;

}

bool MaxHeap::increase_element(int element, int idx)

{

    if(idx > count || idx < 0)

        return false;

    if(arr[idx] > element)

        return false;

    arr[idx] = element;

    // the below code is same as insert

    // repeating it, to be clear

    while(idx > 0 && arr[PARENT(idx)] < arr[idx]) {

        int tmp=arr[PARENT(idx)];

        arr[PARENT(idx)] = arr[idx];

        arr[idx] = tmp;

        idx = PARENT(idx);

    }

    return true;

}

bool MaxHeap::decrease_element(int element, int idx)

{

    if(idx > count || idx < 0)

        return false;

    if(element > arr[idx])

        return false;

    arr[idx]= element;

    max_heapify(arr, idx, count);

    return true;

}

bool MaxHeap::change(int element, int idx)

{

    if(idx > count || idx < 0)

        return false;

    if(element > arr[idx] )

        return increase_element(element, idx);

    else

        return decrease_element(element, idx);

}

void main()

{

    MaxHeap obj;

    int A[] = {7,2,1,12,15,8,4,0,6,13,9,5};

    for(int i=0; i<12;i++) {

        obj.insert(A[i]);

    }

    int val;

    obj.remove(val);

    obj.increase_element(20, 5);

    obj.decrease_element(3, 0);

    obj.change(80, 8);

    obj.change(0, 0);

}

Important points

• change does both increase, decrease
• max_heapify is reused